Másodlagos indexek

Az elsődleges indexel, a fizikai elrendezés adta lehetőséget elhasználtuk. Ennek ellenére van lehetőségünk további indexek létrehozására. Nyilvánvalóan az e célra létrehozott segédstruktúrákat is tárolnunk kell, de mivel csak mutatókat fogunk tárolni az adatra, ezért az a tárhely igény a tábla méretéhez képest elhanyagolható.

Sűrű index

Minden rekordot egy mutatót rendelünk, melyeket szekvenciálisan az adott oszlop(okban) szereplő értékek szerint rendezve tárolunk.

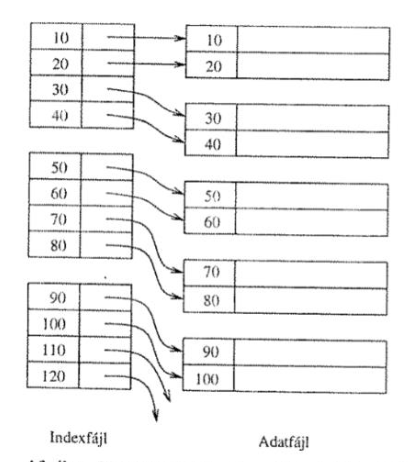
Ritka index

A sűrű indexhez nagyon hasonló, de rekordok helyett blokkokra tárolunk mutatókat. A rendezés alapjául szolgáló kulcs az adatblokkban szereplő első rekord megadott oszlopának (esetleg oszlopainak) értéke.

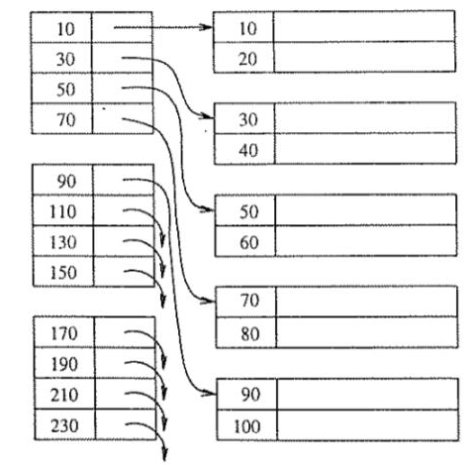
Többszintű index

Az indexre is tudunk indexet készítene, mellyel tovább tudjuk növelni a hatékonyságot.

információ

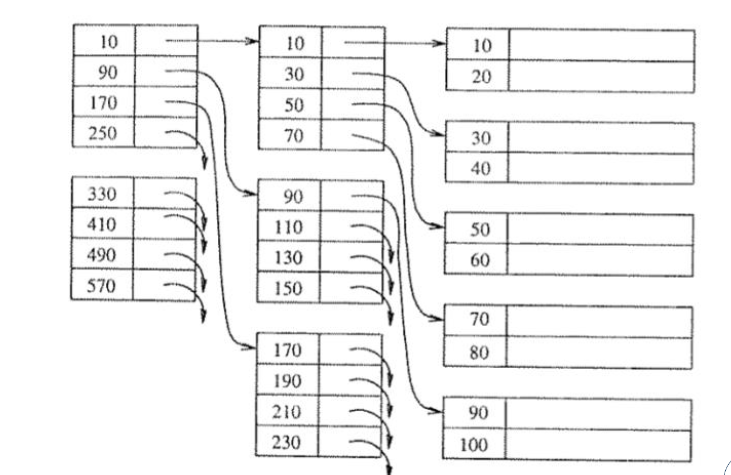
Többszintű index esetén csak az alsó szint lehet sűrű. Ez logikus, hiszen bármely azonos oszlopra készített sűrű index pontosan ugyanazokat a mutatókat tartalmazza (legfeljebb a sorrendjük tér el [stabil rendezés esetén még ez sem]).

Indexek tárhelyigénye

Az indexek tárhelyigényének vizsgálatához vezessük be a következő fogalmakat:

• $\mathrm{T}{(R)}$: az $R$ reláció sorainak száma
• $\mathrm{B}{(R)}$: az $R$ reláció tárolásához szükséges blokkok száma
• blokkolási faktor:
  • $\mathrm{bf}{(R)}$: azt adja meg az $R$ reláció hány sora fér el egy blokkban
  • $\mathrm{bf}{(I)}$: azt adja meg az $I$ index hány kulcs-érték párja fér el egy blokkban

Példa

Legyen $R$ táblák, sűrű $I_1$ és ritka $I_2$ indexek úgy, hogy $\mathrm{T}{(R)} = 10000$, $\mathrm{bf}{(R)} = 20$, $\mathrm{bf}{(I_1)} = 100$, $\mathrm{bf}{(I_2)} = 100$. Számoljuk ki hány blokk szükséges az említett struktúrák tárolásához.

$$\mathrm{B}{(R)} = \frac{\mathrm{T}{(R)}}{\mathrm{bf}{(R)}} = \frac{10000}{20} = 500$$

Mivel $I_1$ egy sűrű index ezért mind a 10000 rekordra el kell tárolnunk 1-1 mutatót:

$$\mathrm{B}{(I_1)} = \frac{\mathrm{T}{(R)}}{\mathrm{bf}{(I_1)}} = \frac{10000}{100} = 100$$

Mivel $I_2$ egy irtka index ezért minden blokkra kell csak mutatót tárolnunk:

$$\mathrm{B}{(I_2)} = \frac{\mathrm{B}{(R)}}{\mathrm{bf}{(I_2)}} = \frac{500}{100} = 5$$

Példa

Oldjuk meg az előző feladatot úh, hogy csak a blokkok $80\%$-a legyen tele!

Ez pontosan azt jelenti, hogy $20\%$-al kevesebb rekord vagy kulcs-mutató pár fér egy blokkba. Így $\mathrm{bf}{(R)} = 16$, $\mathrm{bf}{(I_1)} = 80$, $\mathrm{bf}{(I_2)} = 80$.

$$\begin{align*} \mathrm{B}{(R)} &= \frac{\mathrm{T}{(R)}}{\mathrm{bf}{(R)}} = \frac{10000}{16} = 625 \\ \mathrm{B}{(I_1)} &= \frac{\mathrm{T}{(R)}}{\mathrm{bf}{(I_1)}} = \frac{10000}{80} = 125 \\ \mathrm{B}{(I_2)} &= \frac{\mathrm{B}{(R)}}{\mathrm{bf}{(I_2)}} = \frac{625}{80} = 7,8125 \approx 8 \\ \end{align*}$$

veszély

Tároláshoz mindig egész blokkok vannak használva, tehát ha egy index mérete 7,0005 blokk lenne az index ténylegesen 8 blokkot fog elfoglalni.

:::